Нам понядобятся библиотеки:
library(tidyverse) # обработка данных
library(sysfonts) # шрифты
library(showtext) # шрифты
library(ltm) # более простая библиотека, которую мы используем для двумерных моделей
library(mirt) # для общих случаев классификации в рамках IRT
library(corrr) # статистика
showtext_auto()
# Если вы ещё не загрузили замечательный шрифт HSE Sans, самое время это сделать. Нужно просто...
#GET('https://github.com/ETymch/Econometrics_2023/raw/main/Plotting/HSESans-Regular.otf', write_disk('HSESans-Regular.otf', overwrite = T))
#GET('https://github.com/ETymch/Econometrics_2023/raw/main/Plotting/HSESans-Bold.otf', write_disk('HSESans-Bold.otf', overwrite = T))
#GET('https://github.com/ETymch/Econometrics_2023/raw/main/Plotting/HSESans-Italic.otf', write_disk('HSESans-Italic.otf', overwrite = T))
#GET('https://github.com/ETymch/Econometrics_2023/raw/main/Plotting/HSESans-SemiBold.otf', write_disk('HSESans-SemiBlod.otf', overwrite = T))
font_add(family = 'HSE Sans',
regular = "HSESans-Regular.otf",
bold = 'HSESans-Bold.otf',
italic = 'HSESans-Italic.otf',
bolditalic = 'HSESans-SemiBlod.otf'
)
Мотивация
Допустим, мы хотим ранжировать таксистов по характеристике - сколько они зарабатывают. Мы - робкие исследователи, спросить про зарплату напрямую мы постеснялись. Зато мы спросили о том, сколько в среднем длится рабочий день с вариантами:
- А1: 1-4 часа
- A2: 5 - 7 часов
- A3: 8 -10 часов
- A4: более 10 часов
И спросили о том, сколько дней в неделю человек работает.
Мы предполагаем, что заработная плата растёт с каждым последующим вариантом ответа. Как нам на основании ответов на эти два вопроса сопоставить людей в выборке?
Скорее всего, вам пришёл в голову простой, но действенный алгоритм, который активно использовался до середины ХХ века. Идея простая - мы просто складываем индекс ответа на первый и второй вопрос. Например, таксист указал, что работает по 8-10 часов в день, индекс равен 3 (А3), а также, что он работает 4 дня в неделю (индекс = 4). Итого, для этого человека характеристика (заработная плата) = 7. Это не значит, что он зарабатывает 7 тысяч рублей, это значит, что он зарабатывает больше, чем человек, который работает 5 часов в день 3 дня в неделю (2 + 3 = 5), потому что . Такой незамысловатый способ называется классической теорией тестов, CTT.
Этот метод используется до сих пор учёными-экономистами. Статьи, которые используют его для построенных оценок характеристик публикуют в престижных журналах, например вот. Тем не менее, у него есть существенные минусы:
- Характеристика не растёт линейно в зависимости от выбранного варианта ответа. А данная модель этого не учитывает.
- такой метод предполагает, что вопросы одинаковы по сложности и равнозначны в том, как они помогают определить характеристику. В прикладных задачах это чаще всего неверно.
Чтобы решить эти проблемы, статистики придумали Item Response Theory (IRT).
Сделаем небольшое лирическое отступление о терминологии. Сама по себе IRT — это не какое-то ноу-хау социологов и психологов (хотя некоторыми оно может так представляться). Всё это - старая история с задачей классификации, которая решается при помощи логит и пробит моделей. Да, IRT – это просто вариация на тему того, что мы используем различные спецификации логистической функции (с 1 параметром, с двумя, особо продвинутые используют спецификации с 3-мя и даже 4-мя параметрами). В экономике модели, похожие на irt чаще всего обобщают и называют задачами классификации/кластеризации, иногда уточняют, называют ordered probit models или как-то ещё. Да, современный статистический аппарат не унифицирован и это большая проблема, особенно для междисциплинарных исследований, потому что возникает ненужная путаница.
Давайте вспомним интуицию, которая стоит за логистической функцией.
Пусть у нас есть человек, которых мы хотели бы классифицировать на основании какой-то ненаблюдаемой характеристики. Тогда для пары следующих за другом вопросов мы должны придумать функцию, которая имеет значение от 0 до 1. Чем выше (ниже) значение ненаблюдаемой характеристики, тем ближе значение функции к 1 (0). Т.е. функция монотонна относительно характеристики. Круто, если у нас есть какое-то пороговое значение характеристики, например, зарплата , при которой все люди работают 8 часов и более. Тогда эти варианты ответа отлично получается разграничить на основании ненаблюдаемой характеристики (см. график.)
# Простая функция - индикатор.
Fx <- function(x, theta){
ifelse(x < theta, 0, 1)
}
# Интервалы по оси х.
x <- seq(-3, 3, by = 0.01)
# Табличка и график:
tibble(x,
Fx = Fx(x,0.5)
) %>%
ggplot(aes(x = x,
y = Fx)) +
geom_line(color = '#533344', linewidth = 2) +
theme_minimal(base_family = 'HSE Sans') +
theme(
panel.grid.major.x = element_blank(), # убираем ненужную разметку
panel.grid.minor.x = element_blank(),
panel.grid.minor.y = element_blank(),
plot.title = element_text(hjust = 0.5)
) +
labs(x = 'Значение характеристики',
y = 'Значение функции',
title = 'В идеале мы хотели бы что-то такое',
subtitle = 'Пороговое значение характеристики = 0.5')
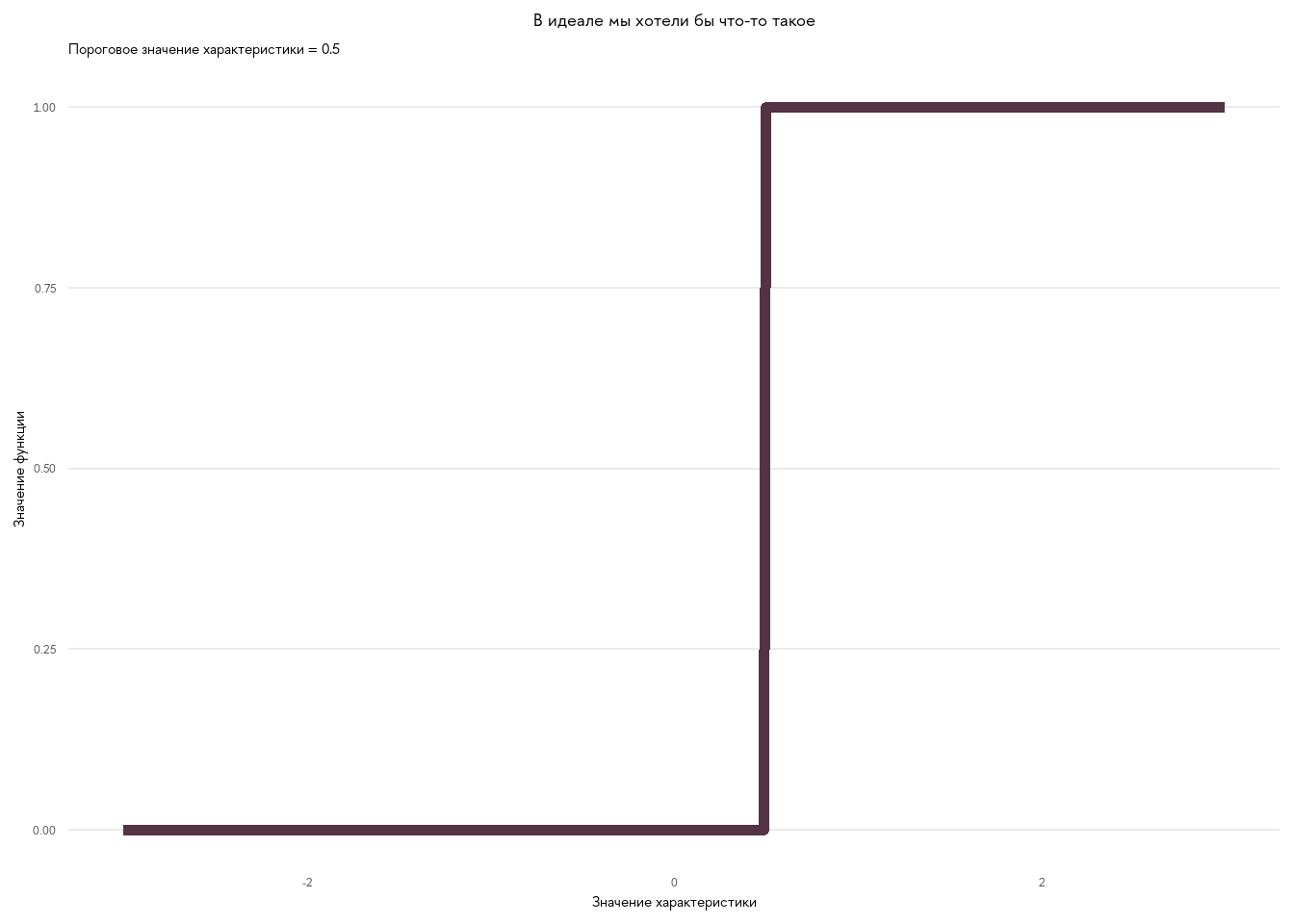
В жизни, к сожалению, таких идеальных вопросов не существует. Поэтому функция более плавно переходит между 0 и 1. Идею вы поняли, вот строгая запись такой логистической функции с двумя параметрами:
Т.е у каждого человека с индексом есть какая-то скрытая характеристика, которую мы хотели бы измерить. Пусть мы задаём этому человеку вопрос и ответ значит, что на вопрос он ответил правильно. Параметр можно интерпретировать как сложность вопроса. Чем больше параметр - тем лучше вопрос позволяет оценить различие в характеристике между людьми. Как вы заметили, в данной модели не имеет индекса, а значит для всех вопросов параметр имеет одинаковое значение. Это, конечно, упрощение, от которого мы избавимся позднее. Пока давайте посмотрим, что происходит с функцией при изменении параметров и и получим дополнительную интуицию, посмотрим, как изменяется форма кривой, если мы увеличиваем а. Чем больше модуль а, тем лучше модель (вопрос) дискриминирует между людьми.
Если a мы можем интерпретировать, как точность, с которой вопрос разделяет людей на группы (или кластеры - кому как нравится), то b - это сложность вопроса. Если вопрос сложнее, то чтобы не него ответить правильно (или выбрать более высокий по рангу ответ), нужно иметь большее значение скрытой характеристики. Всё становится понятнее, если взглянуть на анимацию.
Об оценивании. Допустим, у нас n возможных вариантов ответа на вопрос. Чтобы оценить то, как изменяется характеристика в зависимости от выбранного ответа, мы можем оценить попарно (для каждых двух ответов, стоящих друг за другом) эти параметры a и b. Например, у нас 4 возможных варианта ответа. Каждый последующий предполагает большее значение характеристики. Тогда мы оцениваем параметры для 2-го варианта ответа против 1-го, 3-го против 2-го и 4-го против 3-го. Если у нас 5 вопросов, то мы проделываем ту же операцию для всех вопросов. Итого, у нас оценено параметров. Иногда параметров в моделях многовато и, чтобы их оценить, нужно использовать марковские цепи.
Как играть в эти модели
Теперь, когда основные идеи более-менее понятны, давайте разберём пару примеров. Лучший способ разобраться - самому оценить такую модель несколько раз на разных примерах. Первый пример - тестирование в рамках экзамена. Скрытая (ненаблюдаемая) характеристика ученика - понимание изучаемого предмета. Экзамен - способ оценить эту ненаблюдаемую штуку и ранжировать студентов в зависимости от понимания. Например, экзамен [GRE](https://ru.wikipedia.org/wiki/GRE_(%D1%82%D0%B5%D1%81%D1%82) для решения такой задачки использует именно IRT модели.
Пример 1: бинарные ответы
data("LSAT")
head(LSAT) # Модели мы будем скармливать табличку с 5-ю переменными, принимающими значения 0 или 1.
## Item 1 Item 2 Item 3 Item 4 Item 5
## 1 0 0 0 0 0
## 2 0 0 0 0 0
## 3 0 0 0 0 0
## 4 0 0 0 0 1
## 5 0 0 0 0 1
## 6 0 0 0 0 1
Для моделирования в рамках IRT есть две хороших библиотеки: более простая - ltm, и более сложная и комплексная mirt. Первую я предлагаю использовать для введения в вопрос, с помощью неё мы оценим модели, в которых ответ на вопрос принимает 2 возможных значения, 0 или 1 (верно/неверно, да/нет). Оценим три модели - с одним параметром, с двумя и стремя.
model_1pl <- ltm::rasch(LSAT, IRT.param = T)
model_2pl <- ltm::ltm(LSAT ~ z1, # один скрытый параметр. см. описание функции, details
IRT.param = T)
model_3pl <- tpm(LSAT,
type = 'latent.trait',
IRT.param = T
)
Очень советую посмотреть описание к каждой модели в справке:
?ltm::rasch
?ltm::ltm
?ltm::tpm
В первой модели оцениваются 6 параметров. Параметр , о котором я рассказывал выше, одинаковый для всех вопросов. Вопросы отличаются по сложности и у каждого вопроса параметр - разный. Такая модель называется моделью Rasch, она достаточно простая, но она уже держится на меньшем количестве предположений, чем классическая теория, где мы просто складывали правильные ответы и получали итоговый счёт.
coef(model_1pl)
## Dffclt Dscrmn
## Item 1 -3.6152665 0.7551347
## Item 2 -1.3224208 0.7551347
## Item 3 -0.3176306 0.7551347
## Item 4 -1.7300903 0.7551347
## Item 5 -2.7801716 0.7551347
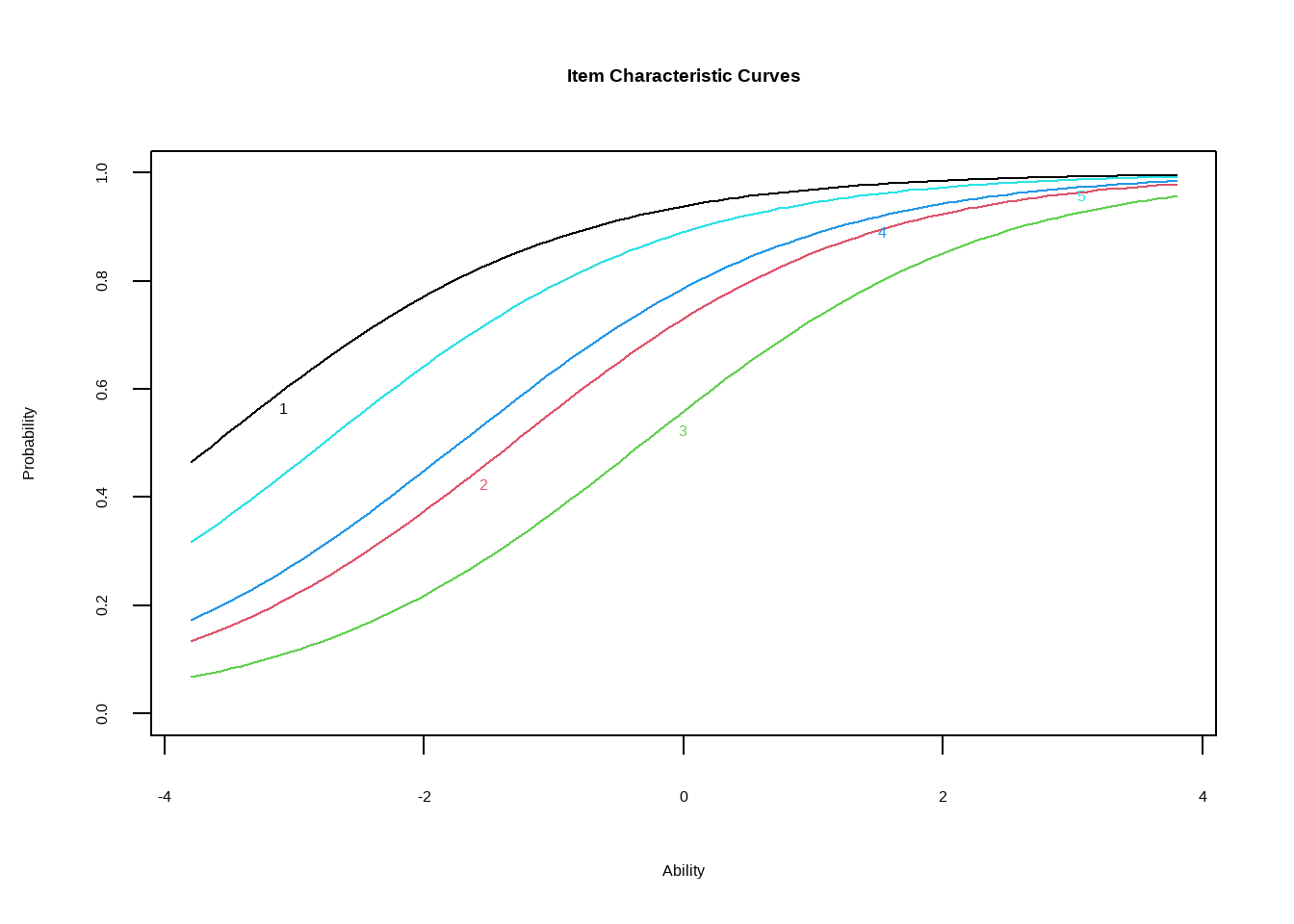
Заметьте, что третий вопрос - самый сложный из пяти, потому что параметр для него наибольший.
Вторая модель оценивает 10 параметров. Теперь у каждого вопроса свой .
coef(model_2pl)
## Dffclt Dscrmn
## Item 1 -3.3597341 0.8253715
## Item 2 -1.3696497 0.7229499
## Item 3 -0.2798983 0.8904748
## Item 4 -1.8659189 0.6885502
## Item 5 -3.1235725 0.6574516
В модели с тремя уникальными параметрами для каждого вопроса добавляется параметр, характеризующий уровни угадывания в каждом вопросе. Я не рассказывал о нём, но если интересно, можете получить интуицию, запустив itemplot(shiny = T). Откроется окно, в котором вы сможете поиграть с различными комбинациями параметров, чтобы получить интуицию.
coef(model_3pl)
## Gussng Dffclt Dscrmn
## Item 1 0.048943967 -3.4298905 0.7843851
## Item 2 0.001670895 -1.3718976 0.7189605
## Item 3 0.372430618 0.6530852 23.2030040
## Item 4 0.017067266 -1.9278300 0.6471598
## Item 5 0.020325411 -2.9562883 0.6913157
Визуализируем первую модель. Согласно оценённым параметрам, третий вопрос самый сложный - его кривая лежит правее прочих.
plot(model_1pl)
На мой взгляд, инструменты визуализации для этой библиотеки - не самые лучшие. Конечно, если вы просто проводите диагностику результатов, вам этого хватит, но для экспорта итогов в приличном виде лучше вытащить из модели параметры и построить график в ggplot2. Это очень просто.
# Функция:
S <- function(x,a,b){
exp(a *(x - b)) / (1 + exp(a *(x - b)))
}
# Оценённые параметры
x <- seq(-8, 5, by = 0.01)
a <- coef(model_1pl)[1,2]
b1 <- coef(model_1pl)[1,1]
b2 <- coef(model_1pl)[2,1]
b3 <- coef(model_1pl)[3,1]
b4 <- coef(model_1pl)[4,1]
b5 <- coef(model_1pl)[5,1]
# График
tibble(theta = x,
f1 = S(x, a, b1),
f2 = S(x, a, b2),
f3 = S(x, a, b3),
f4 = S(x, a, b4),
f5 = S(x, a, b5),
) %>%
pivot_longer(f1:f5) %>%
ggplot(aes(x = theta, y = value, color = name)) +
geom_line() +
theme_minimal(base_family = 'HSE Sans') +
theme(panel.grid.major.x = element_blank(), # убираем ненужную разметку
panel.grid.minor.x = element_blank(),
panel.grid.minor.y = element_blank(),
legend.position = 'bottom',
axis.title.y = element_blank()
)
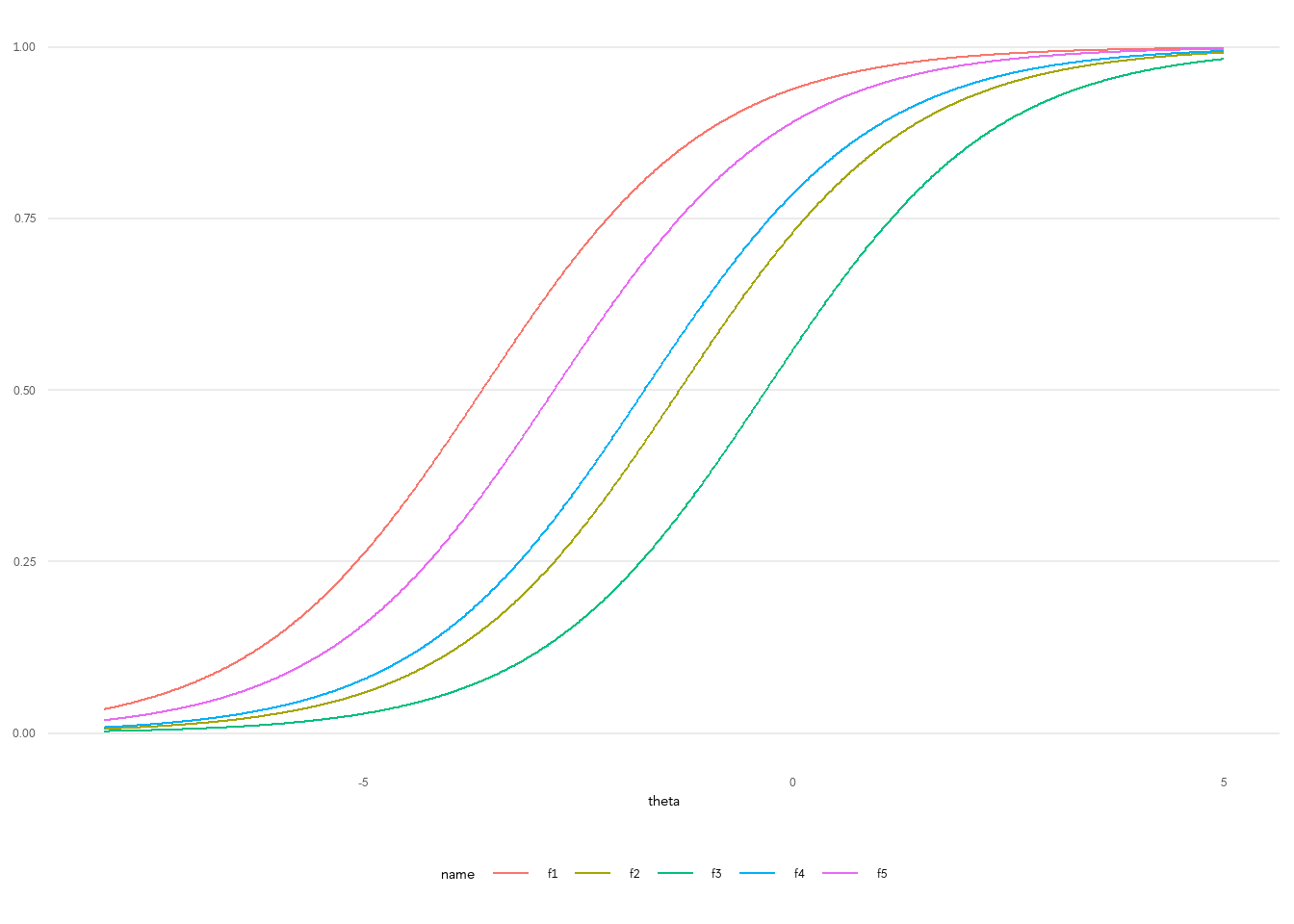
Для воторой и третьей модели постройте графики самостоятельно.
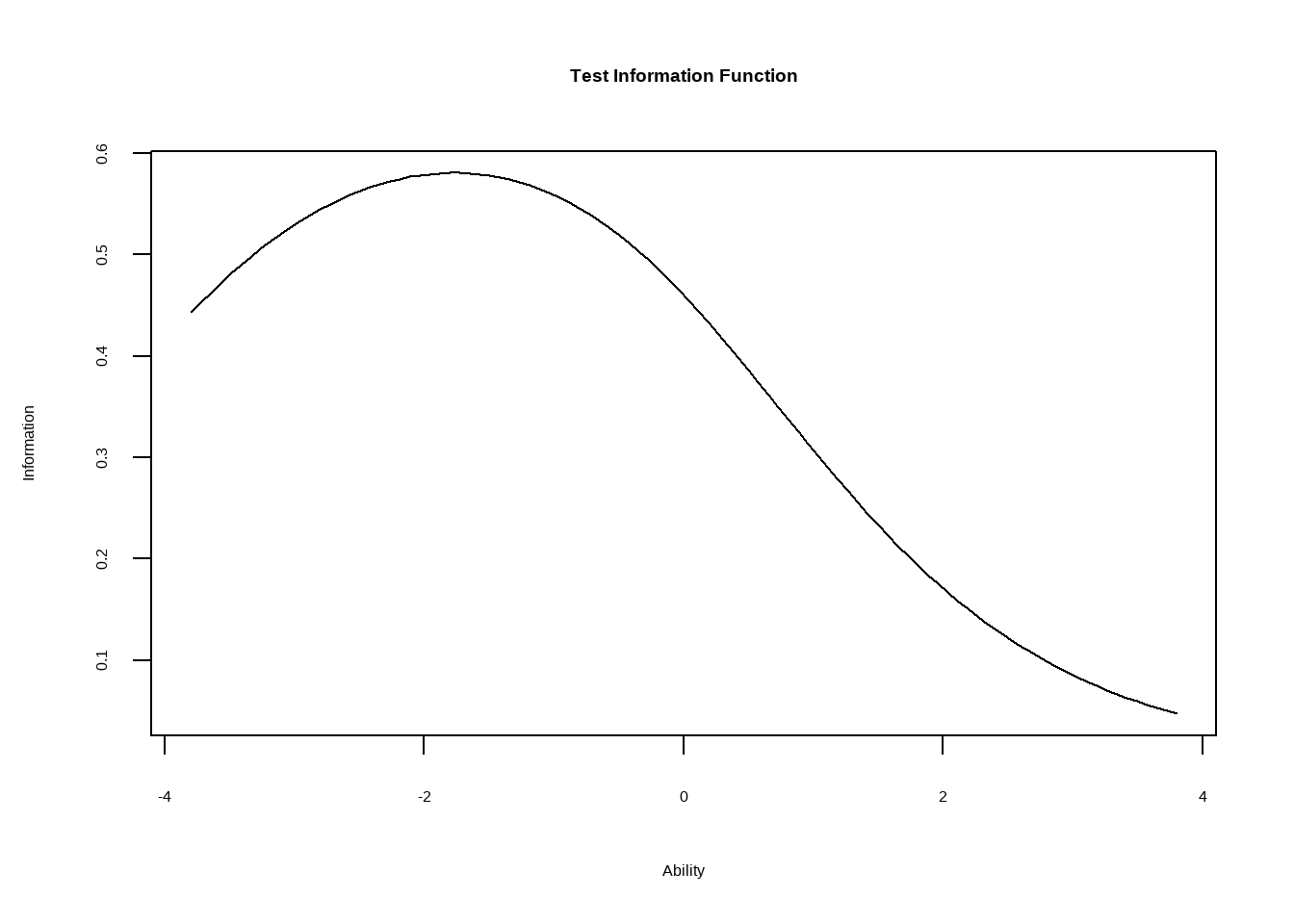
Другая полезная визуализация - распределение скрытого параметра, которое мы можем определить, задав 5 вопросов в выборке. Из-за того, что вопросы достаточно простые, распределение сдвинуто влево.
model_2pl %>%
plot(type = 'IIC', items = 0)
Значения скрытой характеристики для людей в выборке:
model_2pl %>% factor.scores() %>% head()
## $score.dat
## Item 1 Item 2 Item 3 Item 4 Item 5 Obs Exp z1 se.z1
## 1 0 0 0 0 0 3 2.277412 -1.89534389 0.7954828
## 2 0 0 0 0 1 6 5.860769 -1.47931399 0.7960948
## 3 0 0 0 1 0 2 2.595854 -1.45960554 0.7962002
## 4 0 0 0 1 1 11 8.942200 -1.04106133 0.8002327
## 5 0 0 1 0 0 1 0.696143 -1.33148746 0.7970643
## 6 0 0 1 0 1 1 2.613638 -0.91144001 0.8022274
## 7 0 0 1 1 0 3 1.178613 -0.89141657 0.8025692
## 8 0 0 1 1 1 4 5.954726 -0.46324210 0.8121527
## 9 0 1 0 0 0 1 1.839822 -1.43779861 0.7963253
## 10 0 1 0 0 1 8 6.431288 -1.01902420 0.8005455
## 11 0 1 0 1 1 16 13.577167 -0.57334915 0.8092633
## 12 0 1 1 0 1 3 4.370280 -0.44053303 0.8127859
## 13 0 1 1 1 0 2 2.000392 -0.41997250 0.8133702
## 14 0 1 1 1 1 15 13.919929 0.02262829 0.8284444
## 15 1 0 0 0 0 10 9.479934 -1.37282610 0.7967513
## 16 1 0 0 0 1 29 34.616474 -0.95330371 0.8015421
## 17 1 0 0 1 0 14 15.589528 -0.93331522 0.8018644
## 18 1 0 0 1 1 81 76.561538 -0.50612525 0.8109917
## 19 1 0 1 0 0 3 4.658812 -0.80310821 0.8041869
## 20 1 0 1 0 1 28 24.988589 -0.37270468 0.8147533
## 21 1 0 1 1 0 15 11.462553 -0.35204385 0.8153752
## 22 1 0 1 1 1 80 83.541023 0.09315984 0.8312672
## 23 1 1 0 0 0 16 11.254471 -0.91118576 0.8022316
## 24 1 1 0 0 1 56 56.105456 -0.48348162 0.8115991
## 25 1 1 0 1 0 21 25.646007 -0.46298152 0.8121599
## 26 1 1 0 1 1 173 173.310387 -0.02195986 0.8267166
## 27 1 1 1 0 0 11 8.445440 -0.32915286 0.8160765
## 28 1 1 1 0 1 61 62.519552 0.11695886 0.8322437
## 29 1 1 1 1 0 28 29.126701 0.13852205 0.8331388
## 30 1 1 1 1 1 298 296.692872 0.60635243 0.8546241
##
## $method
## [1] "EB"
##
## $B
## [1] 5
##
## $call
## ltm::ltm(formula = LSAT ~ z1, IRT.param = T)
##
## $resp.pats
## [1] FALSE
##
## $coef
## Dffclt Dscrmn
## Item 1 -3.3597341 0.8253715
## Item 2 -1.3696497 0.7229499
## Item 3 -0.2798983 0.8904748
## Item 4 -1.8659189 0.6885502
## Item 5 -3.1235725 0.6574516
Пример 2: Модели со множественными вариантами ответов
Пример и данные взяты отсюда, я лишь немного дополнил это своим кодом. Теперь мы будем использовать библиотеку mirt. К библиотеке прилагается замечательная справка, ?mirt.
data_doom <- read.csv('https://raw.githubusercontent.com/doomlab/learnSEM/master/vignettes/data/lecture_irt.csv') %>%
na.omit() %>% # 10 вопросов, везде ответы от 1 до 7
mutate(Q99_9 = 8 - Q99_9) %>% # Автор сказала изменить эту переменную потому что она упорядочена задом-наперёд.
dplyr::select(Q99_1, Q99_4, Q99_5, Q99_6, Q99_9)
gpcm_doom <- mirt(data_doom,
model = 1, # z1 - число скрытых переменных
itemtype = 'gpcm') # graded partial credit model (gpcm) - тип модели, в которой у каждого вопроса свой коэффициент а, и внутри вопроса разные b
coef(gpcm_doom, IRTpars = T) # Если ответы хорошо последовательны, то параметры b увеличиваются слева направо.
## $Q99_1
## a b1 b2 b3 b4 b5 b6
## par 1.924 -1.903 -1.344 -1.107 -0.607 0.226 1.236
##
## $Q99_4
## a b1 b2 b3 b4 b5 b6
## par 2.938 -1.951 -1.67 -1.082 -0.592 0.121 0.973
##
## $Q99_5
## a b1 b2 b3 b4 b5 b6
## par 2.393 -2.051 -1.601 -1.255 -0.825 -0.093 0.98
##
## $Q99_6
## a b1 b2 b3 b4 b5 b6
## par 2.445 -2.013 -1.43 -1.168 -0.531 0.118 1.086
##
## $Q99_9
## a b1 b2 b3 b4 b5 b6
## par 0.553 -1.677 -2.487 -1.201 -0.113 -1.114 -0.295
##
## $GroupPars
## MEAN_1 COV_11
## par 0 1
Основной диагностический график в моделях со множеством вариантов ответа выгладит так. Не пугайтесь, сейчас всё станет понятно. На горизонтальной оси показана скрытая характеристика, . Если увеличивается, то вероятность выбрать вопрос с большим индексом тоже увеличивается (если характеристика монотонно возрастает по индексам). Посмотрите на вопрос Q99_6. Для каждого варианта ответа существует такой уровень скрытой характеристики, при котором этот вариант ответа наиболее вероятен. Значит этот вопрос хорошо различает людей по характеристике, он хороший, он нам полезен. Теперь посмотрите на вопрос Q99_9. Для него условие, которое я описал выше не выполняется, он не очень хорошо распределяет людей, нужно посмотреть, что с ним не так, в что с ним не так. Проблема в том, что он не упорядочен, если посмотреть на параметры внутри вопроса, то с увеличением индекса (сложность) не растёт, значит ответы плохо упорядочены.
plot(gpcm_doom, type = 'trace')
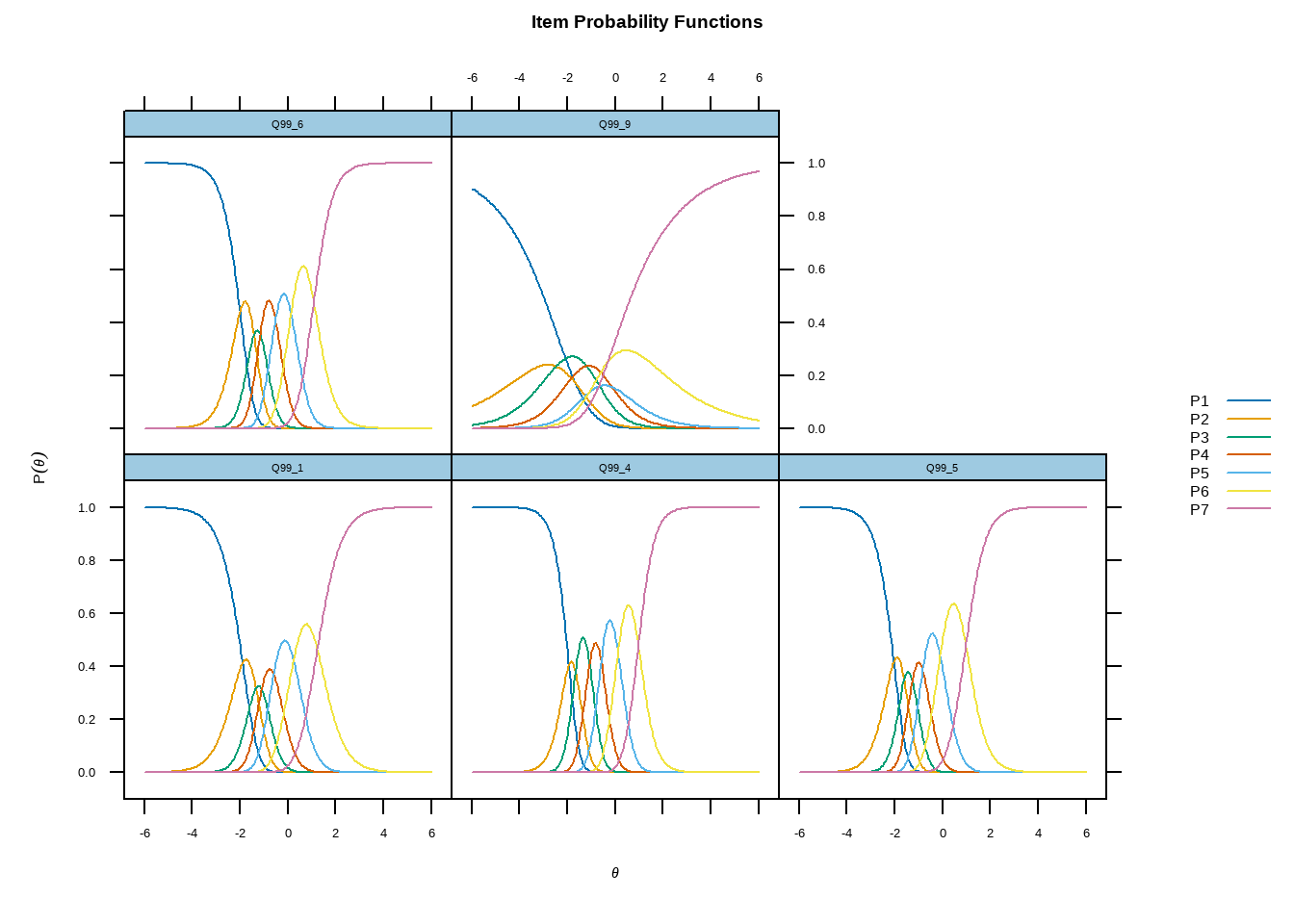
Так же, как и в прошлом примере, данный график показывает, что на основании этих вопросов нам куда сложнее различить людей с высокими значениями скрытой характеристики, чем людей с низкими значениями таковой.
plot(gpcm_doom, type = 'info')
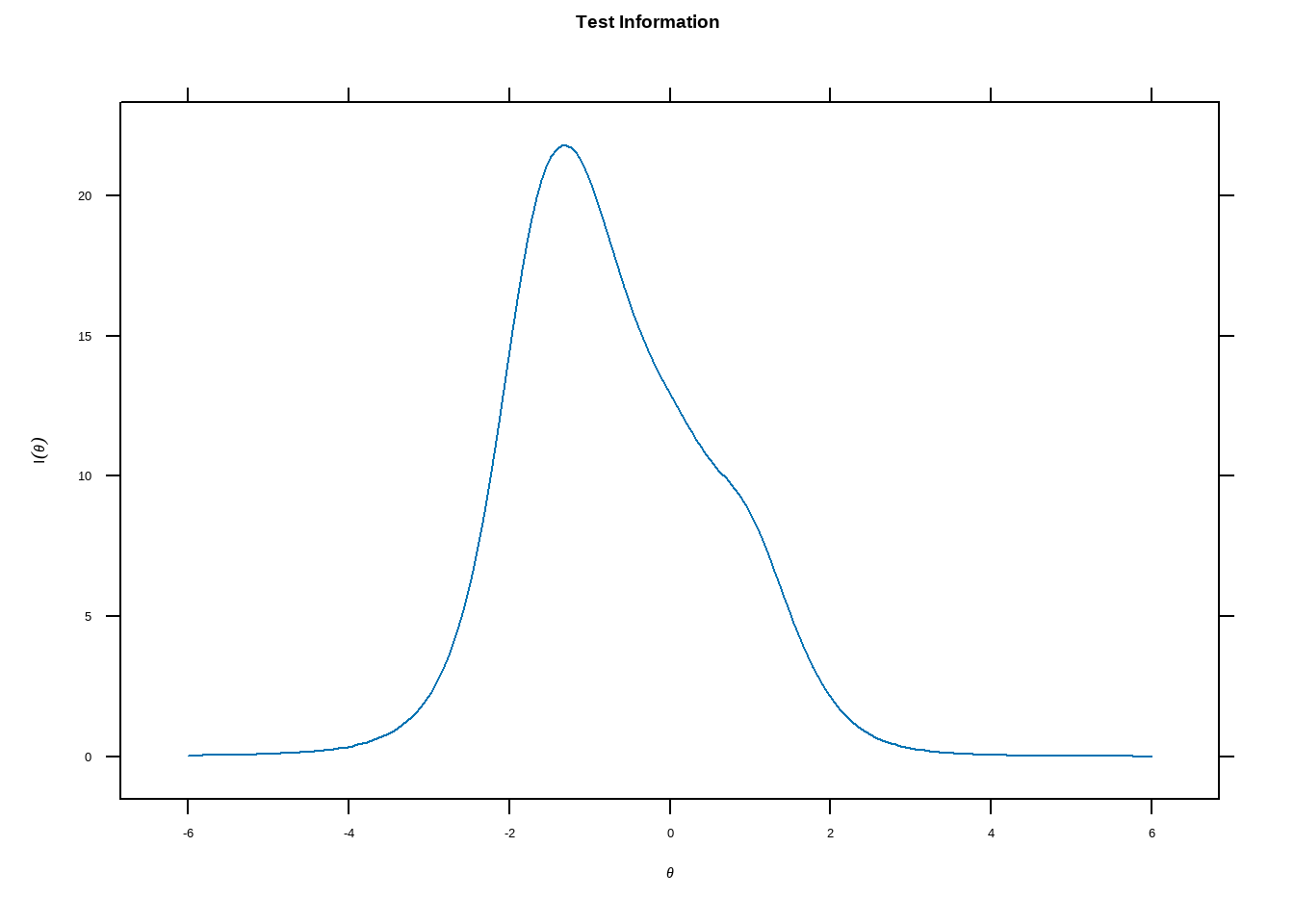Значения скрытой характеристики для каждого человека можно получить так:
fscores(gpcm_doom) %>% head()
## F1
## [1,] -0.6801705
## [2,] -2.7479553
## [3,] -1.2484923
## [4,] -1.4224606
## [5,] -2.7479553
## [6,] -2.7479553
Попробуйте оценить gpcm для оставшихся пяти вопросов в выборке . Поиграйте, попробуйте выбрать другую модель из списка, , сравните оцениваемые параметры и прогнозы, которые дают разные модели.
Пример 3: Зарплата курьеров
Сейчас мы проверим, насколько хорошо работают разные методы. У нас есть данные с ответами на вопросы, которые связаны с заработной платой, но не дают прямого ответа. Среди них вопросы об:
- Образовании,
- средней длительности рабочего дня,
- длительности рабочей недели,
- используемом на работе виде транспорта
Более того, у нас есть “истинные” (декларируемые в опросе) данные о зарплате. Таким образом, мы попробуем использовать несколько методов ранжирования людей в выборке (по ненаблюдаемой зп) и посмотрим, какой из методов был точнее.
Загрузим уже обработанные данные.
data_kuryery <- read.csv('https://raw.githubusercontent.com/ETymch/Econometrics_2023/main/Datasets/data_opros.csv') # Из опроса курьеров я отобрал только тех,
# кто разносит продукты, убрал наблюдения с пропусками.
data_kuryery %>% head(10)
## Q3 Q6 Q9 Q26 Q12
## 1 3 3 4 3 10
## 2 4 4 3 3 12
## 3 4 4 3 3 12
## 4 4 4 3 3 12
## 5 4 2 3 1 9
## 6 3 2 4 2 3
## 7 4 3 2 1 3
## 8 4 4 1 2 2
## 9 2 3 3 1 4
## 10 1 2 1 3 2
# Вопрос Q12 - Сколько вы зарабатываете курьером:
# 1 Менее 5 тыс
# 2 5-10 тыс. р
# 3 10-20 тыс. р
# 4 20-30 тыс. р
# 5 30-40 тыс. р
# 6 40-50 тыс. р
# 7 50-60 тыс. р
# 8 60-70 тыс. р
# 9 70-80 тыс. р
# 10 80-90 тыс. р
# 11 90-100 тыс. р
# 12 100-120 тыс. р
# 13 120-150 тыс. р
# 14 150-200 тыс. р # Да, бывают и такие курьеры.
Табличка, которую мы скормим программе - оставим только вопросы.
data_quest <- data_kuryery %>%
dplyr::select(Q3, # Вопрос - сколько дней в неделю вы работаете? 1 день ~ 1. 2-3 ~ 2. 4-5 ~ 3. 6-7 ~ 4.
Q6, # На каком виде транспорта вы работаете? Пешком ~ 1. Велосипед ~ 2. Электросамокат/электровелосипед ~ 3. Автотранспорт ~ 4.
Q9, # Сколько часов в день вы работаете? 1-4 ~ 1. 5-7 ~ 2. 8-11 ~ 3. >12 ~ 4.
Q26 # # Уровень образования. Среднее ~ 1. Среднее специальное ~ 2. Высшее ~ 3. Несколько высших/учёная степень ~ 4.
)
# Оценим 5 моделей разными способами. Чтобы получить справку по каждой модели, используйте ?mirt.
model_rasch <- mirt(data_quest,
itemtype = 'Rasch',
method = 'SEM')
model_grsm <- mirt(data_quest,
itemtype = 'grsm',
method = 'SEM')
model_gpcm <- mirt(data_quest,
itemtype = 'gpcm',
method = 'SEM')
model_ggum <- mirt(data_quest,
itemtype = 'ggum',
method = 'SEM')
model_monopoly <- mirt(data_quest,
itemtype = 'monopoly',
method = 'SEM')
Опытным путём я пришёл к тому, что для оценки параметров на практике лучше использовать алгоритм Stochastic EM (expectation maximization), нежели просто EM. Из-за сложности модели, оцениваемые простым EM, часто не сходятся, но оценивание при помощи SEM занимает чуть больше времени.
На сей раз опустим этап, на котором мы строили диагностические графики (по-хорошему это нужно было бы сделать, но статья не резиновая), просто визуализируем результаты.
# Собираем всё в одну табличку
results <- tibble(rasch = fscores(model_rasch) %>% c(), # прогнозы каждой модели
grsm = fscores(model_grsm) %>% c(),
gpcm = fscores(model_gpcm) %>% c(),
ggum = fscores(model_ggum) %>% c(),
monopoly = fscores(model_monopoly) %>% c(),
ctt = data_quest %>% apply(1, sum), # прогноз на основе классической теории тестов. Помните метод, в котором мы просто складывали ответы на вопросы и получали итоговый счёт? Вот это он.
true = data_kuryery$Q12
)
Визуализация:
palette <- c('#003f5c', '#444e86', '#955196', '#dd5182', '#ff6e54', '#ffa600')
results %>%
pivot_longer(rasch:ctt) %>%
ggplot(aes(x = as.factor(true), y = value, color = name)) +
geom_point(position = position_jitterdodge(), alpha = 0.2) +
facet_wrap(~name, scales = 'free') +
geom_boxplot(alpha = 0.25, size = .9) +
scale_color_manual(values = palette) +
theme_minimal(base_family = 'HSE Sans') +
theme(panel.grid.major.x = element_blank(), # убираем ненужную разметку
panel.grid.minor.x = element_blank(),
panel.grid.minor.y = element_blank(),
legend.position = 'bottom',
axis.title.y = element_blank()
) +
labs(x = 'Заработная плата')
Чем выше значение скрытой характеристики (вертикальная ось), тем выше категория ( в зависимости о зп), в которую попал человек. Обратите внимание, что истинное значение заработной платы в данном случае - просто индекс. Приращение этого индекса не соответствует приращению заработной платы. Чтобы посчитать истинную корреляцию следовало бы представить средние значения заработной платы для данного индекса. Проведём простой тест результатов:
results %>%
correlate() %>%
focus(true)
## # A tibble: 6 × 2
## term true
## <chr> <dbl>
## 1 rasch 0.409
## 2 grsm 0.388
## 3 gpcm 0.437
## 4 ggum -0.397
## 5 monopoly 0.428
## 6 ctt 0.409
Качественно выделяются две модели. Таким образом, мы можем ранжировать людей в зависимости от ожидаемой заработной платы, это открывает обширные возможности для построения количественных моделей, оценки репрезентативности выборки, качества ответов на вопросы и других исследований.
Если вы занимаетесь экспериментами в общественных науках, то обзор литературы об этом можно найти на MIT OCW. Курс покрывает темы, связанные с когнитивными искажениями, как это измерить при помощи крутого дизайна исследования.